Sensor Noise Model Calibration
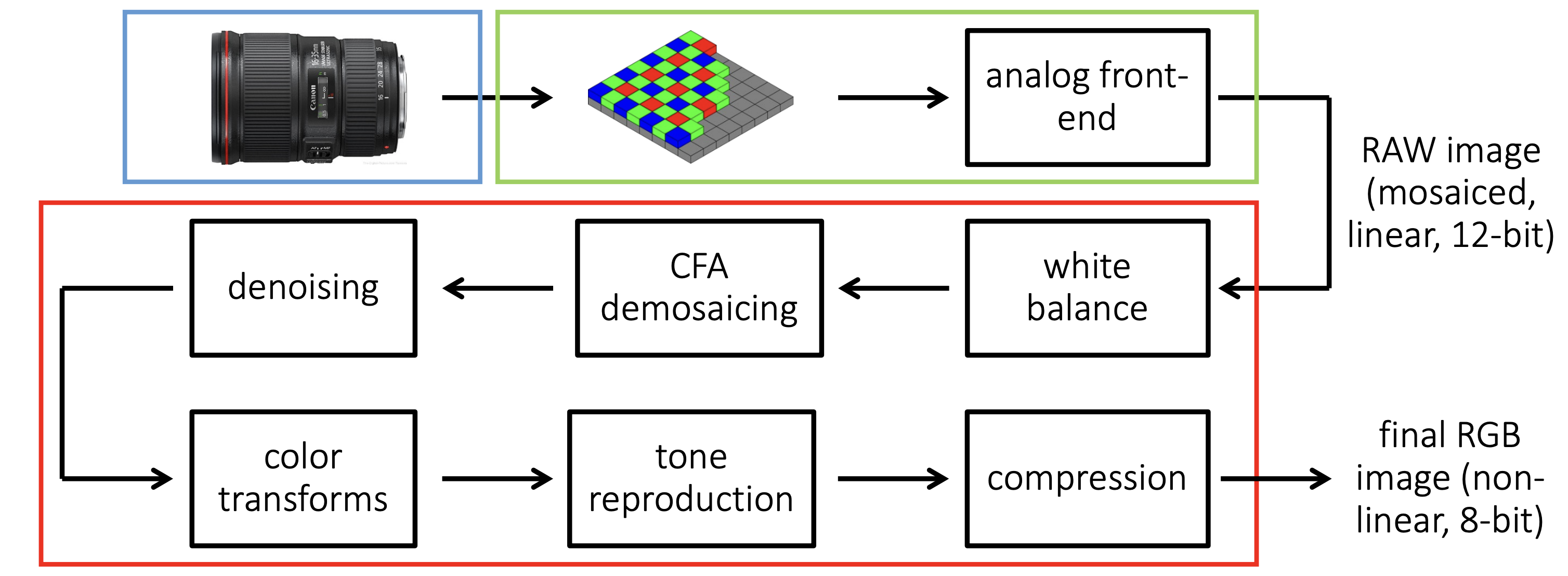
图片来源:CMU Computational Photography, Fall 2020
Pipeline中绿色框部分会引入噪声,具体如下:
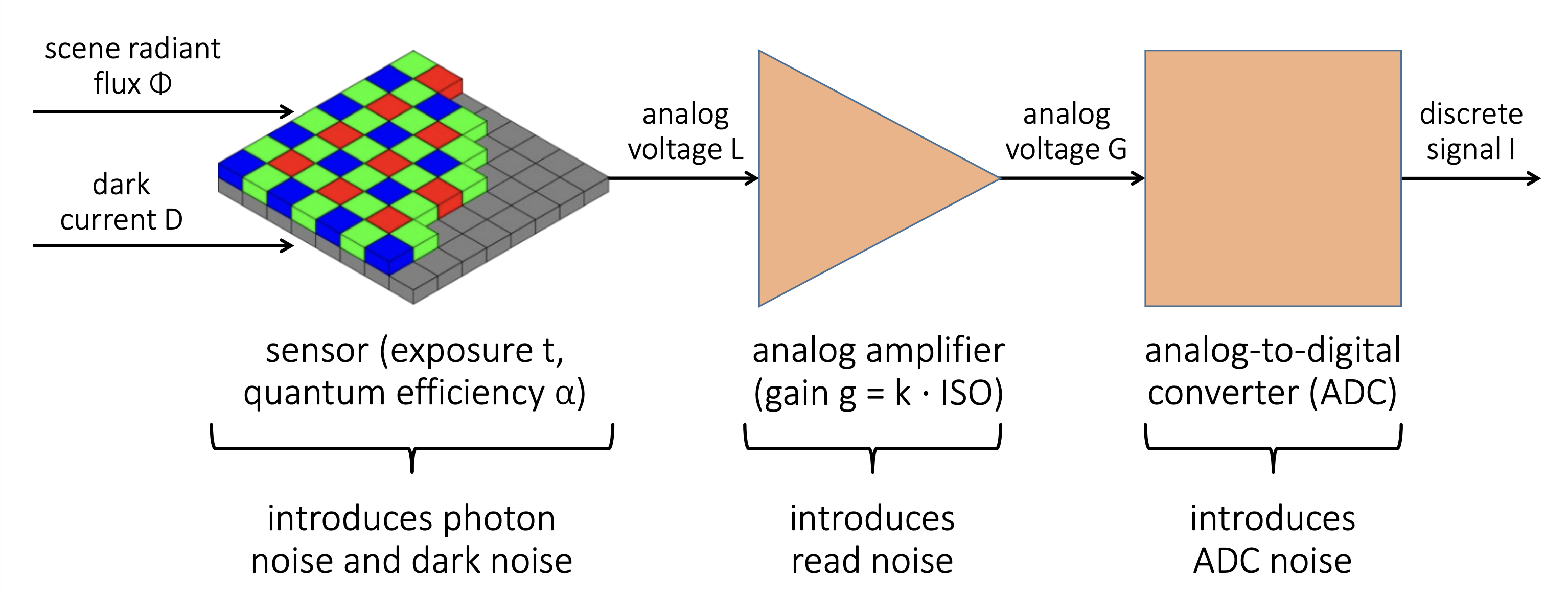
图片来源:CMU Computational Photography, Fall 2020
具体而言会有以下三种noise:
Photon noise,也称Shot noise 光粒子到达的随机性,符合泊松分布
Dark noise
暗电流的影响,即便没有光粒子到达,也会因为元器件本身的特性产生噪声,一般而言温度越高,噪声越大,符合均值0的高斯分布
Read noise
信号放大过程中、模数转换过程中引入的噪声,俗称:gain、ADC;符合均值0的高斯分布
因此可以在Raw denoise的相关论文中找到以下noise model。
\[ x_p \sim N(y_p, \sigma_r^2 + \sigma_s y_p) \]
\[ y \sim N(\mu=x, \sigma^2=\lambda_{read} + \lambda_{shot} x) \to N(\mu=x,\sigma^2=g_d^2\sigma_r^2 + g_dg_ax) \]
其中digital gain \(g_d\), analog gain \(g_a\),read noise的固定方差\(\sigma^2\) \[ \lambda_{read}=g_d^2 \sigma_r^2, \ \lambda_{shot} = g_d g_a \]
以下对上面的噪声联合分布进行推导。
(Photon)Shot noise与环境照度,曝光有关。令环境照度$ $ ,光电转换效率$ $,曝光时间t, 暗电流强度D
Shot noise满足泊松分布 \[ n \sim Possion(\varphi, \alpha, t) = Possion(\varphi \cdot \alpha \cdot t) \] Dark noise与曝光有关,曝光时间越长,元器件温度越高,暗电流影响越大,与环境光无关,满足泊松分布 \[ n \sim Possion(D \cdot t) \] 那么电信号L满足泊松分布,Shot noise和Dark noise的联合分布 \[ L \sim Possion(t \cdot (\alpha \cdot \varphi + D)) \] 信号放大过程中产生Read noise,模数转换过程中产生ADC noise,两种noise满足均值为0的高斯分布
\[ n_{read} \sim Normal(0, \sigma_{read}) \]
\[ n_{ADC} \sim Normal(0, \sigma_{ADC}) \]
电信号L放大后表示为G,放大的增益g,g与ISO有关 \(g = k \cdot ISO\),\(G = L \cdot g + n_{read} \cdot g\),
经过ADC后信号:\(I = G + n_{ADC}\)
最终信号I表示为: \[ I = L \cdot g + n_{read} \cdot g + n_{ADC} \] 计算信号的均值和方差 \[ E(I) = g \cdot E(L) + g \cdot E(n_{read}) + E(n_{ADC}) \] 由于read noise和ADC noise均符合均值为0的高斯分布,因此 \[ E(I) = g \cdot E(L) = g \cdot t \cdot (\alpha \cdot \varphi + D) \] 方差 \[ \begin{aligned} \sigma(I)^2 &= \sigma(L \cdot g)^2 + \sigma(n_{read} \cdot g)^2 + \sigma(n_{ADC})^2 \\ &= g^2 \cdot t \cdot (\alpha \cdot \varphi + D) + g^2 \cdot \sigma(n_{read})^2 + \sigma(n_{ADC})^2 \end{aligned} \] read noise和ADC noise都属于加性噪声,可以合并 \[ I = L \cdot g + n_{read} + n_{ADC} = L \cdot g + n_{Add} \]
\[ n_{Add} = n_{read} \cdot g + n_{ADC} \]
方差可以表示为: \[ \sigma(I)^2 = g^2 \cdot t \cdot (\alpha \cdot \varphi + D) + \sigma(n_{Add})^2 \] 一直暗电流,即:black level,那么可以消除暗电流D \[ E(I) = g \cdot t \cdot (\alpha \cdot \varphi + D) = g \cdot t \cdot (\alpha \cdot 0 + D) = g \cdot t \cdot D \] 估计出暗电流的影响,可以将其从信号中减去,得到以下表达: \[ E(I) = g \cdot t \cdot \alpha \cdot \varphi \]
\[ \begin{aligned} \sigma(I)^2 &= g^2 \cdot t \cdot \alpha \cdot \varphi + \sigma(n_{Add})^2 \\ &= g \cdot E(I) + \sigma(n_{Add})^2 \end{aligned} \]
因此可以看出联合分布的方差是一个线性关系,可与通过最小二乘法进行拟合。
在实际的噪声估计中当做是 \(pixel \ value \to x\),最终得到开头的推导:\(g \to \lambda_{shot}, \sigma(n_{add})^2 \to \lambda_{read} \to g_d^2\sigma_r^2\) \[ y \sim N(\mu=x, \sigma^2=\lambda_{read} + \lambda_{shot} x) \]
实际上,\(\lambda_{read}\)和 \(\lambda_{shot}\)都是与ISO强相关的,在噪声标定1.0版本,需要对ISO 100,300,500,800,1600,3200进行标定,得到RGB三通道\(\lambda_{read}\)和\(\lambda_{shot}\)共3*2*6=36组参数,在其它ISO值时,需要对齐进行插值。可能会引入不必要的误差,因此在噪声标定2.0版本中,将ISO作为参数引入标定过程。针对Sony sensor,有一个比较通用的公式:\(g_d \cdot g_a = \frac{ISO}{100}\),此时我们\(\lambda_{read}\)和\(\lambda_{shot}\)进行二次拟合,拟合的目标如下: \[ \lambda_{shot} = S \cdot g_d \cdot g_a = S \cdot \frac{ISO}{100} \]
\[ \lambda_{read} = R_0 \cdot (g_d \cdot g_a)^2 + R_1 = R_0 \cdot \frac{ISO}{100} + R_1 \]
此时将ISO作为参数引入标定过程,未来在噪声估计时会更精准。
总结不同噪声在不同场景下的主导地位:
| regime | dominant noise | notes |
|---|---|---|
| bright noise | photon noise | scene-dependent |
| dark noise | read and ADC noise | scene-independent |
| low iso | ADC noise | post-gain |
| high iso | photon and read noise | pre-gain |
| long exposure | dark noise | thermal dependence |